Publications

2025

1. arXiv

   

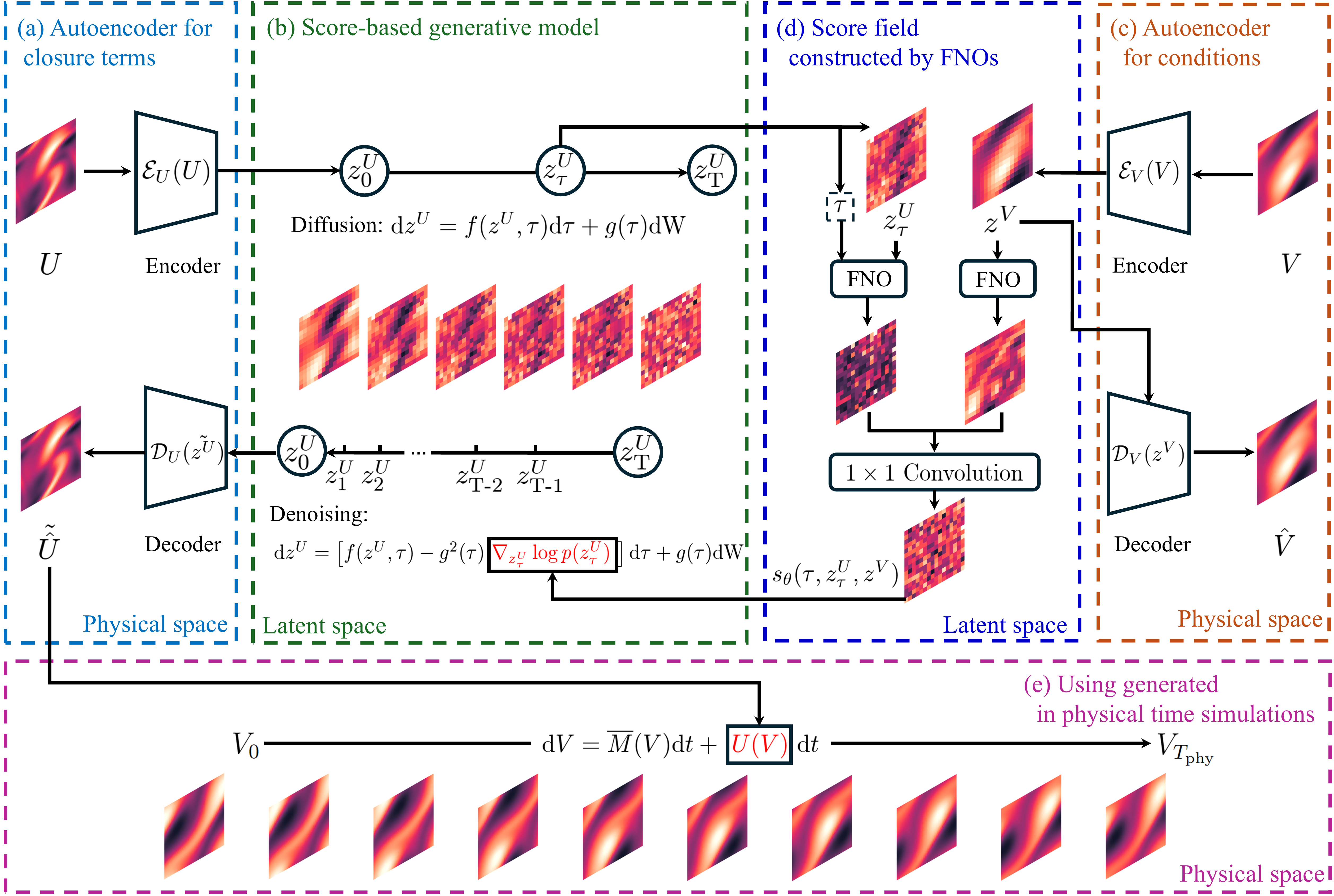   Stochastic and Non-local Closure Modeling for Nonlinear Dynamical Systems via Latent Score-based Generative Models

   Xinghao Dong, Huchen Yang, and Jin-Long Wu

   arXiv preprint arXiv:xxxx.xxxxx, 2025

   Under review in CMAME

   Abs Bib

   We propose a latent score–based generative AI framework for learning stochastic, non-local closure models and constitutive laws in nonlinear dynamical systems of computational mechanics. This work addresses a key challenge of modeling complex multiscale dynamical systems without a clear scale separation, for which numerically resolving all scales is prohibitively expensive, e.g., for engineering turbulent flows. While classical closure modeling methods leverage domain knowledge to approximate subgrid-scale phenomena, their deterministic and local assumptions can be too restrictive in regimes lacking a clear scale separation. Recent developments of diffusion-based stochastic models have shown promise in the context of closure modeling, but their prohibitive computational inference cost limits practical applications for many real-world applications. This work addresses this limitation by jointly training convolutional autoencoders with conditional diffusion models in the latent spaces, significantly reducing the dimensionality of the sampling process while preserving essential physical characteristics. Numerical results demonstrate that the joint training approach helps discover a proper latent space that not only guarantees small reconstruction errors but also ensures good performance of the diffusion model in the latent space. When integrated into numerical simulations, the proposed stochastic modeling framework via latent conditional diffusion models achieves significant computational acceleration while maintaining comparable predictive accuracy to standard diffusion models in physical spaces.

   @article{dong2025efficient,
     author = {Dong, Xinghao and Yang, Huchen and Wu, Jin-Long},
     journal = {arXiv preprint arXiv:xxxx.xxxxx},
     title = {Stochastic and Non-local Closure Modeling for Nonlinear Dynamical Systems via Latent Score-based Generative Models},
     year = {2025},
     note = {<b>Under review in CMAME</b>},
   }

2. arXiv

   

   Bayesian Experimental Design for Model Discrepancy Calibration: An Auto-Differentiable Ensemble Kalman Inversion Approach

   Huchen Yang, Xinghao Dong, and Jin-Long Wu

   arXiv preprint arXiv:2504.20319, 2025

   Under review in JCP

   Abs Bib PDF

   Bayesian experimental design (BED) offers a principled framework for optimizing data acquisition by leveraging probabilistic inference. However, practical implementations of BED are often compromised by model discrepancy, i.e., the mismatch between predictive models and true physical systems, which can potentially lead to biased parameter estimates. While data-driven approaches have been recently explored to characterize the model discrepancy, the resulting high-dimensional parameter space poses severe challenges for both Bayesian updating and design optimization. In this work, we propose a hybrid BED framework enabled by auto-differentiable ensemble Kalman inversion (AD-EKI) that addresses these challenges by providing a computationally efficient, gradient-free alternative to estimate the information gain for high-dimensional network parameters. The AD-EKI allows a differentiable evaluation of the utility function in BED and thus facilitates the use of standard gradient-based methods for design optimization. In the proposed hybrid framework, we iteratively optimize experimental designs, decoupling the inference of low-dimensional physical parameters handled by standard BED methods, from the high-dimensional model discrepancy handled by AD-EKI. The identified optimal designs for the model discrepancy enable us to systematically collect informative data for its calibration. The performance of the proposed method is studied by a classical convection-diffusion BED example, and the hybrid framework enabled by AD-EKI efficiently identifies informative data to calibrate the model discrepancy and robustly infers the unknown physical parameters in the modeled system. Besides addressing the challenges of BED with model discrepancy, AD-EKI also potentially fosters efficient and scalable frameworks in many other areas with bilevel optimization, such as meta-learning and structure optimization.

   @article{yang2025bayesian,
     title = {Bayesian Experimental Design for Model Discrepancy Calibration: An Auto-Differentiable Ensemble Kalman Inversion Approach},
     author = {Yang, Huchen and Dong, Xinghao and Wu, Jin-Long},
     journal = {arXiv preprint arXiv:2504.20319},
     year = {2025},
     note = {<b>Under review in JCP</b>}
   }

3. JCP

   

   Data-driven Stochastic Closure Modeling via Conditional Diffusion Model and Neural Operator

   Xinghao Dong, Chuanqi Chen, and Jin-Long Wu

   Journal of Computational Physics, pp. 114005, 2025

   Abs Bib PDF Code

   Closure models are widely used in simulating complex multiscale dynamical systems such as turbulence and the earth system, for which direct numerical simulation that resolves all scales is often too expensive. For those systems without a clear scale separation, deterministic and local closure models often lack enough generalization capability, which limits their performance in many real-world applications. In this work, we propose a data-driven modeling framework for constructing stochastic and non-local closure models via conditional diffusion model and neural operator. Specifically, the Fourier neural operator is incorporated into a score-based diffusion model, which serves as a data-driven stochastic closure model for complex dynamical systems governed by partial differential equations (PDEs). We also demonstrate how accelerated sampling methods can improve the efficiency of the data-driven stochastic closure model. The results show that the proposed methodology provides a systematic approach via generative machine learning techniques to construct data-driven stochastic closure models for multiscale dynamical systems with continuous spatiotemporal fields.

   @article{dong2025data,
     title = {Data-driven Stochastic Closure Modeling via Conditional Diffusion Model and Neural Operator},
     author = {Dong, Xinghao and Chen, Chuanqi and Wu, Jin-Long},
     journal = {Journal of Computational Physics},
     pages = {114005},
     year = {2025},
     publisher = {Elsevier},
   }

2022

1. arXiv

   Some Numerical Simulations in Favor of the Morrey’s Conjecture

   Xinghao Dong, and Koffi Enakoutsa

   arXiv preprint arXiv:2211.11194, 2022

   Abs Bib PDF

   Morrey Conjecture deals with two properties of functions which are known as quasi-convexity and rank-one convexity. It is well established that every function satisfying the quasi-convexity property also satisfies rank-one convexity. Morrey (1952) conjectured that the reversed implication will not always hold. In 1992, Vladimir Sverak found a counterexample to prove that Morrey Conjecture is true in three dimensional case. The planar case remains, however, open and interesting because of its connections to complex analysis, harmonic analysis, geometric function theory, probability, martingales, differential inclusions and planar non-linear elasticity. Checking analytically these notions is a very difficult task as the quasi-convexity criterion is of non-local type, especially for vector-valued functions. That’s why we perform some numerical simulations based on a gradient descent algorithm using Dacorogna and Marcellini example functions. Our numerical results indicate that Morrey Conjecture holds true.

   @article{dong2022some,
     title = {Some Numerical Simulations in Favor of the Morrey’s Conjecture},
     journal = {arXiv preprint arXiv:2211.11194},
     author = {Dong, Xinghao and Enakoutsa, Koffi},
     year = {2022},
   }