Xinghao Dong(董星浩)
PhD Candidate | MSCS at the University of Wisconsin-Madison.
The Artificial Intelligence for Modeling and Simulation Lab.
Applied Mathematics + Specialization in Computing,
University of California, Los Angeles. The creative principle resides in mathematics. - Albert Einstein
Research: I develop efficient data-driven models for complex systems that are multi-scale, multi-physics, and chaotic in nature. My current research focuses on stochastic modeling using advanced generative approaches, including diffusion models, flow matching, and their variants. I am also interested in nonlocal modeling and continuous spatiotemporal representations.
Previously: I obtained my Bachelor’s degree in Applied Mathematics and Computing from University of California, Los Angeles (UCLA). I spent a few months working on proving the Morrey’s Conjecture by providing several numerical examples.
News
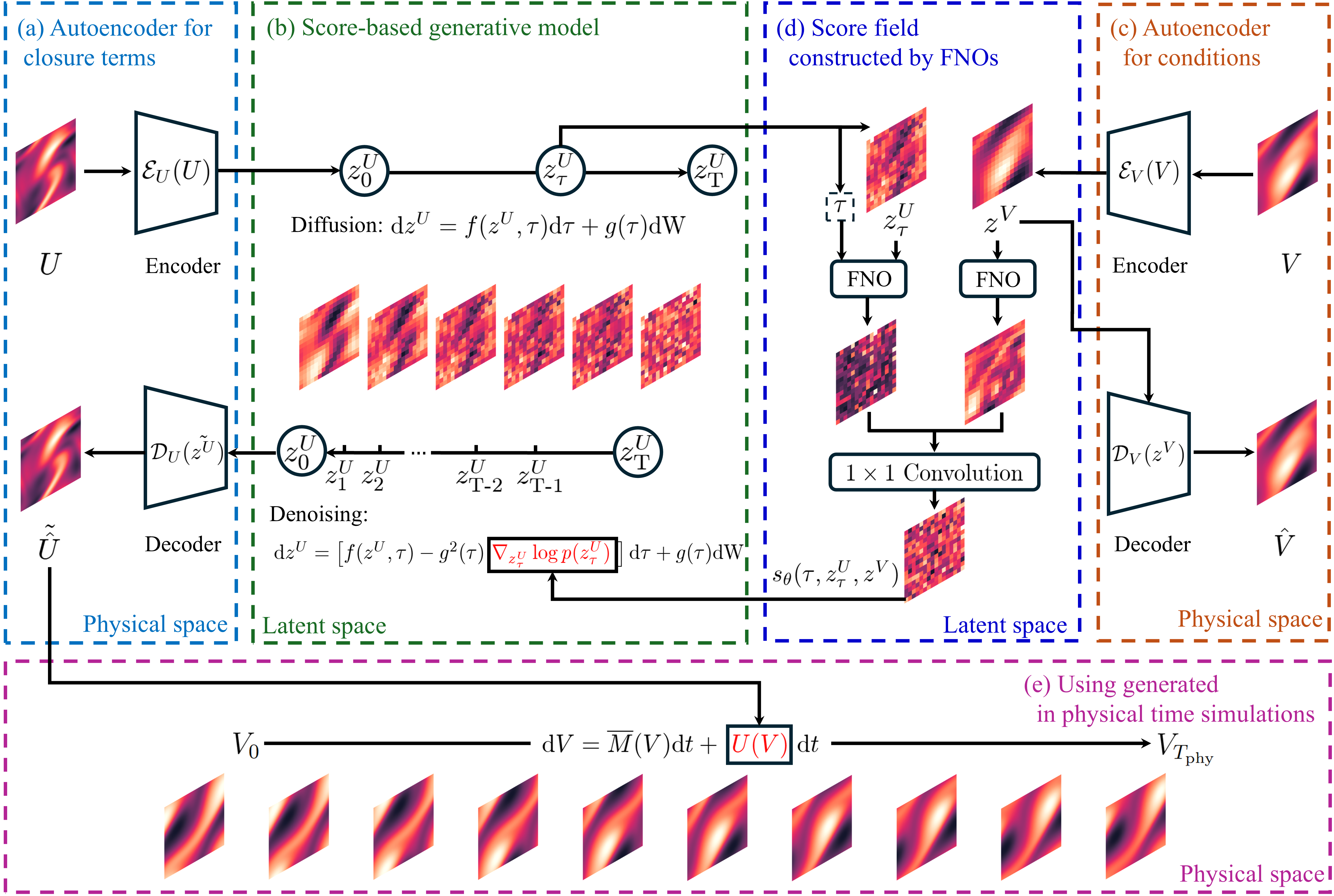
| Apr 14, 2025 | Paper “Data-Driven Stochastic Closure Modeling via Conditional Diffusion Model and Neural Operator” accepted by Journal of Computational Physics. |
|---|---|
| Feb 23, 2025 | Work presented at the DTE & AICOMAS 2025. |
| Dec 13, 2024 | Work presented at the AGU24. |
| Nov 27, 2024 | Work presented at the APS/DFD 2024. Selected for DFD-Interact which features top submissions. |
| Sep 06, 2024 | I have successfully passed my qualification examinations and advanced to candidacy. |